ISMAR 2021|浙江大學和商湯聯合提出適應于挑戰性場景下的視覺慣性里程計
摘要 · 看點
在 ISMAR 2021 上,商湯研究院和浙江大學 CAD&CG 國家重點實驗室合作提出適應于挑戰性場景下的視覺慣性里程計。本工作首先基于深度學習設計了一個魯棒的不依賴視覺的慣性運動跟蹤網絡,接著緊耦合視覺、IMU 和網絡信息,提出了 RNIN-VIO 系統,在安卓手機上實現了整套方案。離線數據集和在線 AR Demo 實驗表明該系統的精度和魯棒性都優于現有方法。
RNIN-VIO: Robust Neural Inertial Navigation Aided Visual-Inertial Odometry in Challenging Scenes1
Danpeng Chen,1,2 Nan Wang,2 Runsen Xu,1 Weijian Xie,1,2 Hujun Bao,1 Guofeng Zhang1*
1State Key Lab of CAD&CG, Zhejiang University 2SenseTime Research and Tetras.AI
Part 1 論文動機
實時的高精度和魯棒的 6DoF 運動跟蹤是增強現實運用的關鍵技術之一。雖然現有的視覺慣性里程計只使用移動平臺上消費級的相機和低廉的 IMU 就能取得比較高的運動跟蹤精度和較優的魯棒性,但是現有視覺慣性里程計仍然依賴連續可靠的視覺跟蹤,在挑戰性場景(如弱紋理、重復紋理、動態環境、快速運動、遠景等)下很容易失效。
Part 2 創新點
1) 提出一個新的基于深度學習的慣性網絡去學習人體運動規律;設計了相對和絕對損失,能讓網絡同時關注到局部精度和全局精度
2) 提出了緊耦合視覺、IMU、慣性網絡測量的多傳感器融合里程計
Part 3 相關工作
目前與本文工作相關的里程計主要分為兩種:視覺慣性里程計和深度學習的 IMU 里程計。
1. 視覺慣性里程計
視覺慣性里程計可以分為基于濾波和基于優化的方法。濾波方法的典型代表是 MSCKF[1]。它使用多狀態卡爾曼濾波融合視覺和 IMU 信息,且將視覺特征零空間化,計算量較低且精度較優。SR-ISWF[2] 是另一種典型的濾波 VIO。由于系統采用均方根的形式,它可以在確保數值穩定情況下,使用單精度浮點去加速運算。優化方法典型代表有 OKVIS[3],VINS-Mono[4]。他們使用優化方法最小化重投影誤差和預積分 IMU 誤差。盡管這些方法已經取得較優的精度和魯棒性,但是在極端視覺場景下,他們仍然容易失效。
2. 深度學習的IMU里程計
這塊主要工作有 IONet[5],RoNIN[6],TLIO[7]。IONet 第一個提出使用 LSTM 網絡直接回歸固定窗口的相對位移和旋轉。RoNIN 假定旋轉已知,用網絡直接回歸窗口平均速度。TLIO 將 RoNIN 網絡改進成 3D 版本,并用 EKF 融合 IMU 測量和網絡測量,取得更高的定位精度。但是這些方法都沒有考慮人類運動在時序上是連續的且有明顯的規律。
Part 4 方法描述
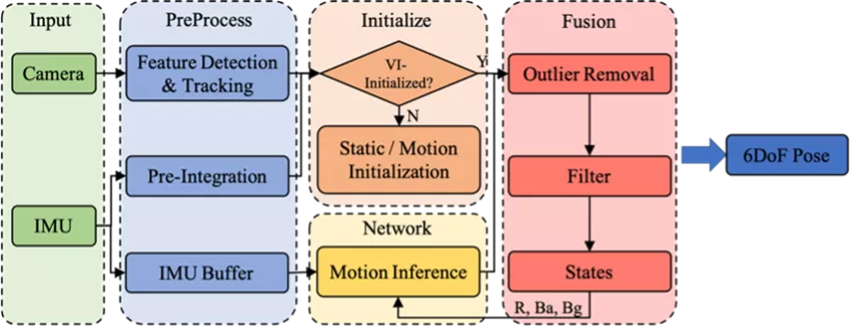
圖1 系統框架
如圖1所示,系統主要包括四部分。預處理,初始化,慣性神經網絡和融合濾波。
預處理:從每幀圖像上提取角點特征,并利用 KLT 進行連續幀圖像跟蹤。連續兩幀圖像之間的 IMU 進行預積分處理。同時我們維護一個 IMU Buffer 作為慣性神經網絡的輸入數據。
初始化:為了讓系統適應各種各樣的運動,當系統檢測到當前是靜止時,采用靜止初始化,若為運動,則采用運動初始化。
慣性神經網絡:慣性神經網絡學習運動的先驗分布。網絡采用一個局部窗口的 IMU 作為輸入,在無需已知初始速度情況下,回歸窗口的相對位移和不確定度。不考慮噪聲情況下,同樣的窗口 IMU 數據,不同初速度對應不同的運動,所以單純靠 IMU 數據是無法估計具體運動的。我們相信盡管運動分布是非常廣闊的,但是人體運動分布應該是非常窄的,同樣的 IMU 數據對應不同的運動應該非常罕見。基于這個考慮,我們相信網絡可以進行合理的運動預測。
融合濾波:濾波系統緊耦合視覺、IMU 和網絡測量信息。其中視覺信息是可以被隨時移除的,這樣系統將變成純 IMU 里程計。

慣性神經網絡
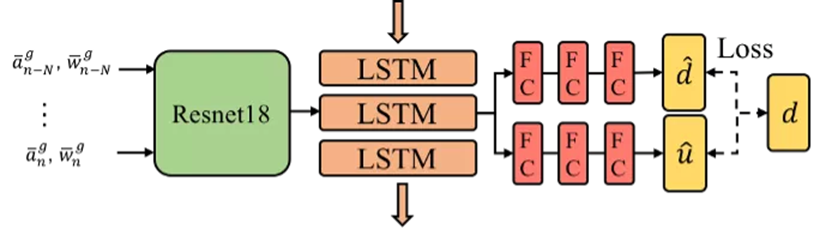
圖2 慣性神經網絡
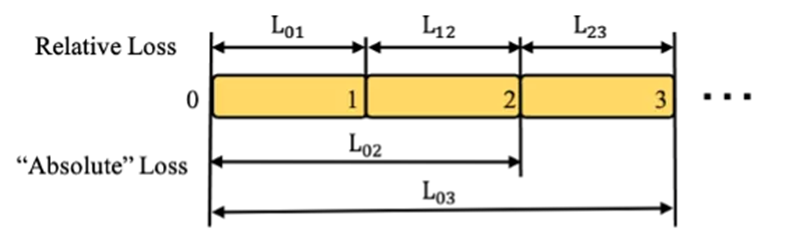
圖3 損失函數
我們設計一個慣性神經網絡去學習人體運動在時序上的規律。我們的網絡架構如圖 2 所示,主要由 1D 版本的 ResNet18, LSTM 和全連接層組成。ResNet 網絡用于學習人體某個動作的隱層特征。我們認為人體運動是連續平滑且有明顯規律的。所以我們使用 LSTM 融合當前動作的隱層特征和之前的隱層特征來估計當前動作最好的隱層特征。最終使用全連接層解碼隱層特征,回歸窗口相對位移和不確定度。
損失函數如圖 3 所示。為了讓網絡能關注到局部精度和更長窗口的絕對精度,我們設計了相應的相對損失和絕對損失函數,后面實驗驗證了損失函數的有效性。
多傳感器融合的6DoF跟蹤
為了構建一個高魯棒,高精度的視覺慣性里程計,我們嘗試把魯棒但低精度的慣性神經網絡測量整合到傳統視覺慣性里程計中。傳統的視覺慣性里程計能估計精確的 IMU 狀態(如位姿,速度,重力方向,偏置等)。通過這些精確的 IMU 狀態可以對原始 IMU 數據進行預處理,給慣性網絡提供更好的輸入數據,提升網絡估計的精度。另外,更精確的網絡估計,能反過來增強系統魯棒性。
視覺慣性里程計大部分模塊和傳統 VIO 類似,這里不再贅述。我們主要講述慣性神經網絡測量能量函數部分。這里有兩點需要特別注意,1、網絡在 yaw 上是旋轉等變性的;2、網絡預測的時間戳不一定和估計狀態的時間戳是對齊的。慣性神經網絡觀測能量函數為:
![]()
由于預測和估計的時間戳不對齊,所以我們使用預積分去對齊時間戳:
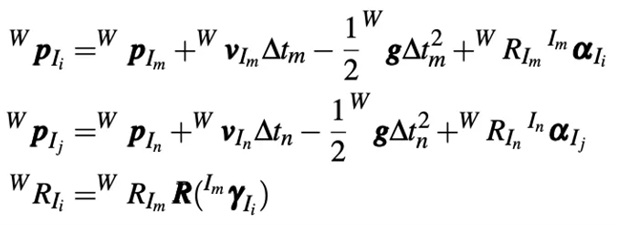
Part 5 實驗結果
我們將提出的方法 RNIN-VIO 和下面方法進行對比: (a) 3D-RoNIN[6], (b) TLIO[7], (c) Ours (wo AL) 是在我們提出的慣性神經網絡基礎上去掉絕對損失函數, (d) BVIO 是我們的RNIN-VIO 系統去掉慣性神經網絡測量, (e) VINS-Mon。
神經網絡部分實驗
我們在開源的 IDOL[8] 數據上測試我們的慣性神經網絡方法和現有方法。同現有方法對比,我們方法取得更高的絕對精度和相對精度。慣性神經網絡也能泛化到不同人、不同設備和不同環境。我們設計的相對損失和絕對損失有效提升網絡整體精度。
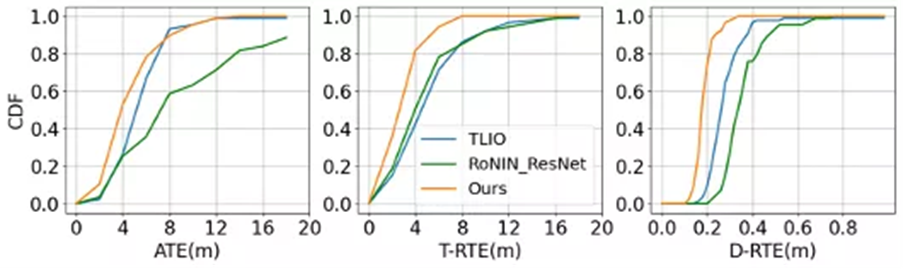
圖4 測試數據集上累積密度函數
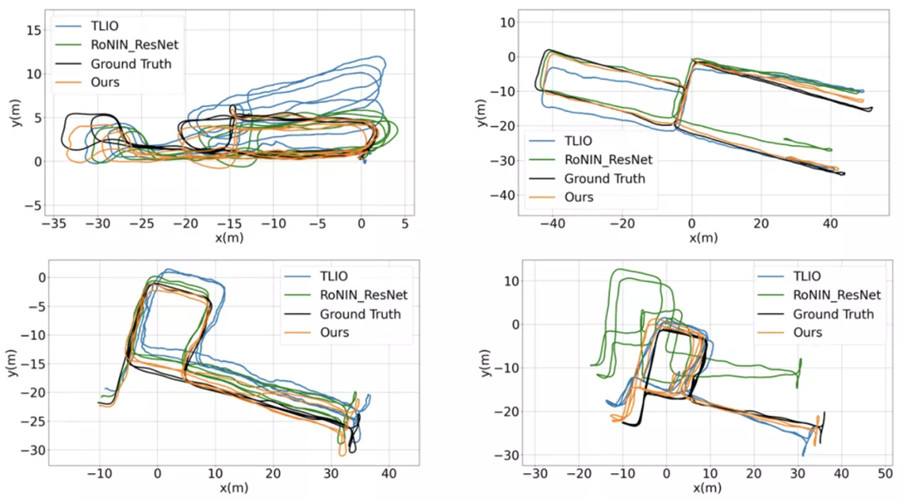
![]()
圖 5 慣性神經網絡估計軌跡圖
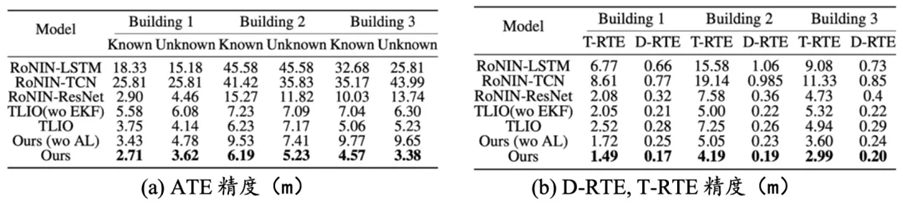
表格 1 神經慣性網絡精度對比
RNIN-VIO 實驗
我們用華為 Mate20 Pro 手機采集了多組室內外數據進行對比。結果表明在正常場景下 RNIN-VIO 和 BVIO 精度接近,而在挑戰性場景下,RNIN-VIO 精度和魯棒性顯著好于 BVIO。
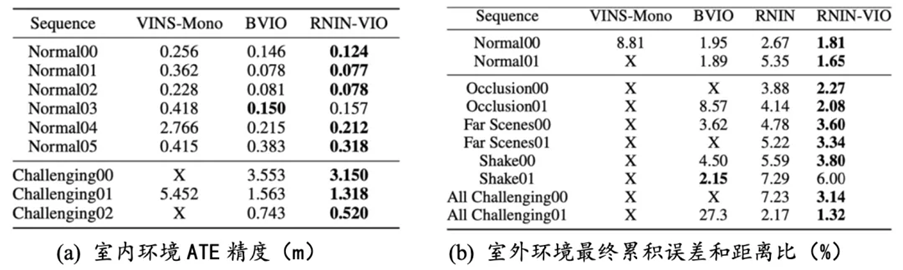
表格2 RNIN-VIO精度對比
Reference:
[1] A.I.MourikisandS.I.Roumeliotis.Amulti-stateconstraintkalman filter for vision-aided inertialnavigation. In Proceedings of IEEE International Conference on Robotics and Automation, pp. 3565–3572. IEEE, 2007.
[2] K. Wu, A. Ahmed, G. A. Georgiou, and S. I. Roumeliotis. A square
root inverse filter for efficient vision-aided inertial navigation on mobile devices. In Robotics: Scienceand Systems, vol. 2, 2015.
[3] S. Leutenegger, S. Lynen, M. Bosse, R. Siegwart, and P. Furgale. Keyframe-based visual–inertialodometry using nonlinear optimization. The International Journal of Robotics Research, 34(3):314–334,2015.
[4] T. Qin, P. Li, and S. Shen. VINS-Mono: A robust and versatile monoc- ular visual-inertial stateestimator. IEEE Transactions on Robotics, 34(4):1004–1020, 2018.
[5] C. Chen, X. Lu, A. Markham, and N. Trigoni. IONet: Learning to cure the curse of drift in inertialodometry. In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, 2018.
[6] S. Herath, H. Yan, and Y. Furukawa. RoNIN: Robust neural inertial navigation in the wild:Benchmark, evaluations, & new methods. In Proceedings of IEEE International Conference on Roboticsand Automation (ICRA), pp. 3146–3152. IEEE, 2020.
[7] W. Liu, D. Caruso, E. Ilg, J. Dong, A. I. Mourikis, K. Daniilidis, V. Kumar, and J. Engel. TLIO: Tightlearned inertial odometry. IEEE Robotics and Automation Letters, 5(4):5653–5660, 2020.
[8] S. Sun, D. Melamed, and K. Kitani. IDOL: Inertial Deep Orientation- Estimation and Localization.arXiv preprint arXiv:2102.04024, 2021.


 返回
返回
 人工智能基礎設施
人工智能基礎設施 企業服務智能化
企業服務智能化 城市管理智能化
城市管理智能化 汽車出行智能化
汽車出行智能化 個人生活智能化
個人生活智能化