CVPR 2020 Oral | DMCP: 可微分的深度模型剪枝算法解讀

模型輕量化是深度學習工業化中一個繞不開的話題。很多神經網絡模型雖然性能很好，但是計算開銷巨大，難以在手機等端上設備高效運行。因此，如何得到計算開銷滿足要求，同時性能也可支撐工業應用的模型一直是大家研究的重點。其中，模型剪枝就是此類方法中比較重要的一項技術。它通過裁剪神經網絡的通道數來降低計算開銷，同時根據特定剪枝算法來選取裁剪掉哪些通道從而降低該過程中的性能損失。在CVPR 2020上，商湯研究院被接收為oral的論文DMCP提出了一種基于馬爾可夫過程的剪枝算法，為模型剪枝提供了新的思路。該工作將模型剪枝建模成了馬爾科夫過程，其中的轉移概率可以通過可微分的方式來進行優化，取得了非常好的效果。

動機

傳統的模型剪枝方法一般分為三步（如圖一所示）：訓練原模型；用剪枝算法剪掉“不重要”的通道；將剪枝后模型參數進行微調。而近年來，有的工作提出剪枝后的模型參數其實并不重要，直接將剪枝模型參數初始化后重新訓練，也可以達到同樣的、甚至更高的精度。因此可以將模型剪枝作為模型結構搜索問題來解決，利用搜索算法搜索出模型每一層的通道數。

圖一 傳統的模型剪枝pipeline

先前的將模型剪枝看作模型結構搜索的工作大多都采用強化學習算法或者遺傳算法，而這些算法需要在原模型中大量的采樣子結構來評估精度，甚至需要花大量時間來訓練子結構，因此很難泛化到更大更復雜的網絡。同時，模型結構搜索問題中也存在此問題。DARTS[1]提出了一種可微分的方法來提高搜索效率。然而這種可謂分的方法不能直接套用在模型剪枝中。首先二者的搜索空間不同，其次DARTS中神經網絡每一層的可選操作是互相獨立的，但是模型剪枝中的選擇隱含著一種互相依賴的關系，例如一層有k+1個通道的話，隱含著這層至少有k個通道。

因此，DMCP選擇將剪枝的過程建模為一個馬爾科夫模型。圖二展示了一層通道數為5的卷積層的剪枝過程。其中S1表示保留第一個通道，S2表示保留第二個通道，以此類推。T表示剪枝完畢。概率p則為轉移概率，通過可學習的參數計算得到，后文中會詳細介紹。

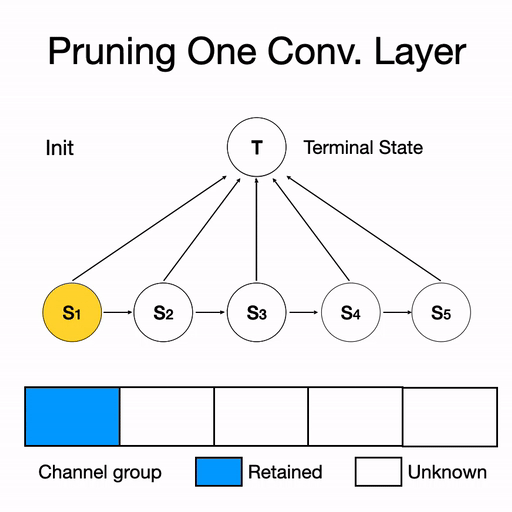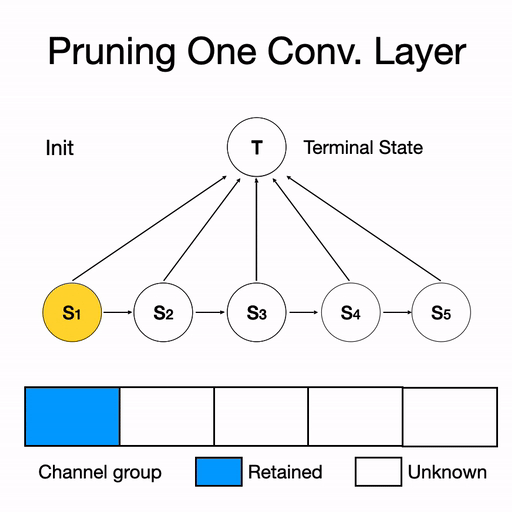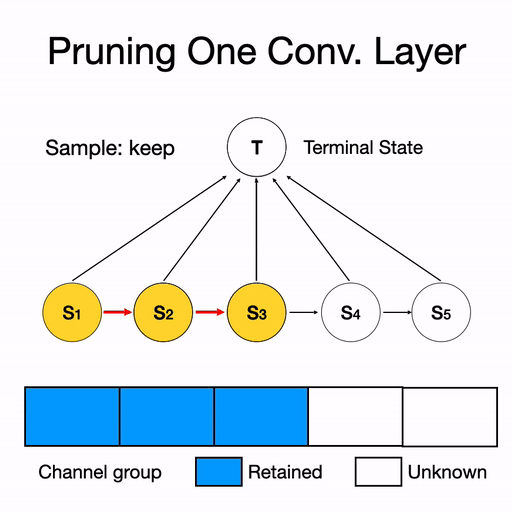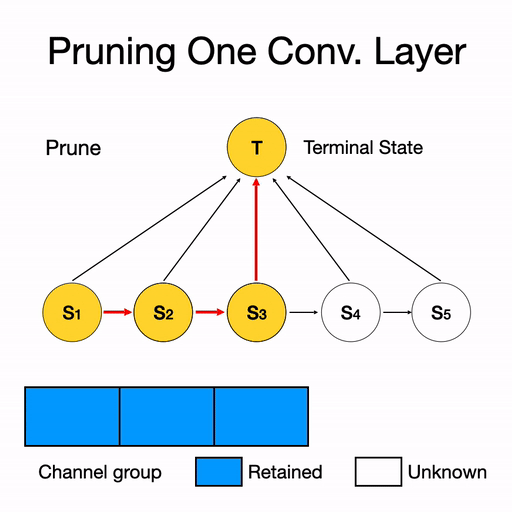
圖二 單層剪枝過程示意圖。

方法

(1) 優化剪枝空間

在傳統的剪枝方法中，會為每個通道計算“重要性”來決定是否保留它。而當我們把模型剪枝看作模型結構搜索問題后，不同模型的區別則在于每一層的通道數量。如果仍然每個通道單獨判斷，就會產生同樣的結構，造成優化困難。如圖三所示：情況1中，最后兩個通道被剪掉，情況2中，第2個和第4個通道被剪掉，而這兩種情況都會產生3個通道的卷積層，使剪枝空間遠大于實際網絡個數。

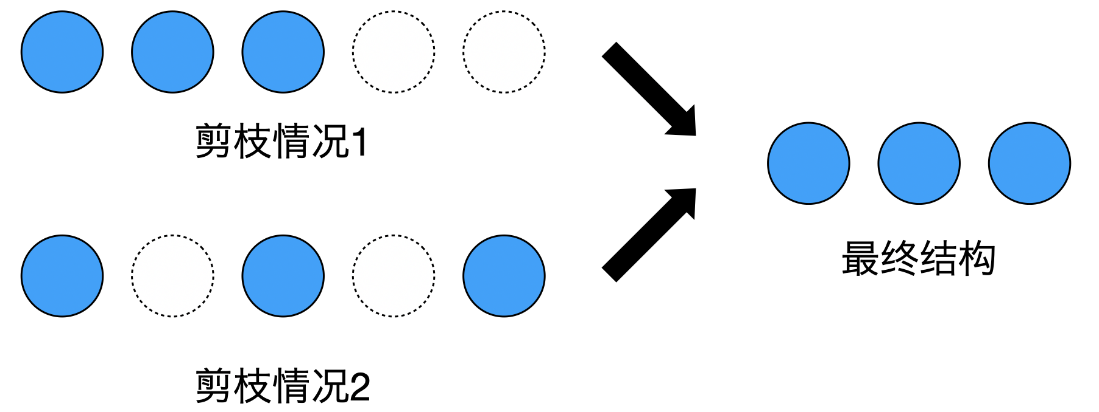
圖三 剪枝空間冗余示意圖

因此，DMCP采用保留前k個通道的方式，大大縮小了剪枝空間。

(2) 建模剪枝過程

在一層卷積層中，定義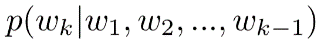為保留前k-1個通道的情況下，保留第k個通道的概率。那么保留前k個通道的概率則為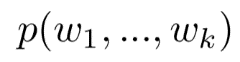，且：

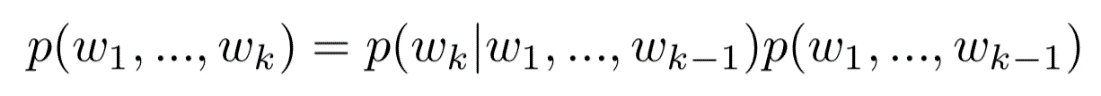（1）

由(1)中的剪枝方式，我們可以得出，已知保留第k-1個通道后，保留前k-2個通道與保留第k個通道條件獨立，且不保留第k-1個通道時，保留第k個通道的概率為0，則有下面的式子成立：

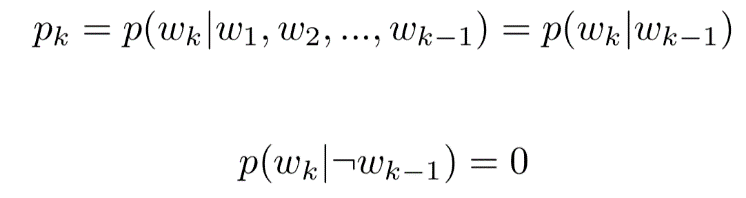（2）

其中pk為馬爾科夫模型中的轉移概率。這樣，通過在優化完畢后的馬爾可夫模型上采樣就可以得到相應的剪枝后的模型。

(3) 學習轉移概率

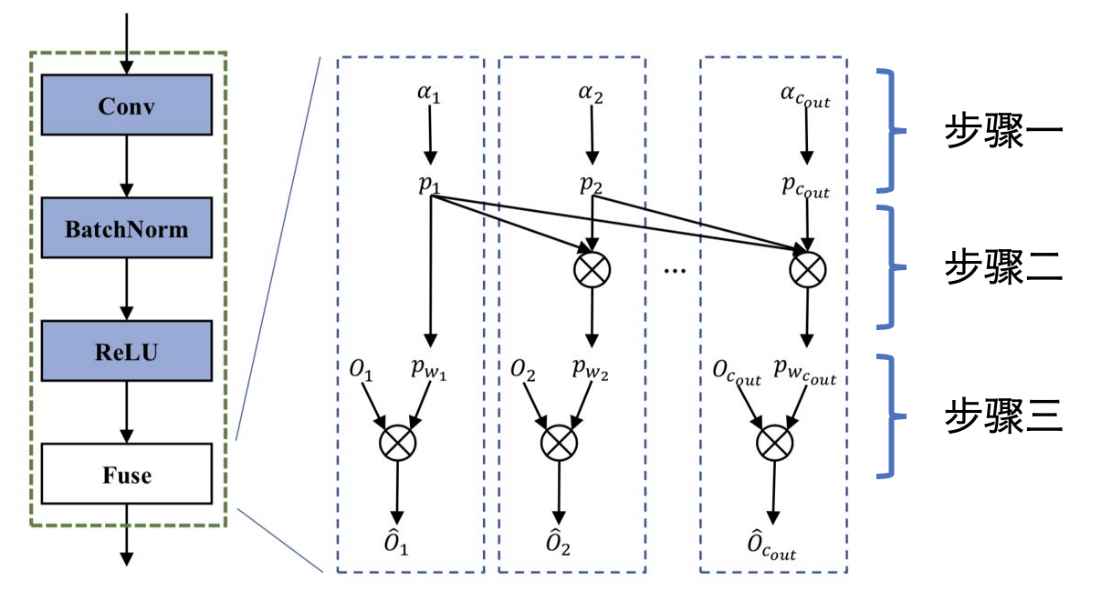
圖四 可微分馬爾可夫模型示意圖

圖四描述了如何將馬爾科夫模型中的轉移概率與原模型進行結合，從而使轉移概率可以通過模型損失函數的梯度來更新。該過程大致可分為三個步驟

步驟一、計算轉移概率pk。

pk可以由如下公式計算得到：

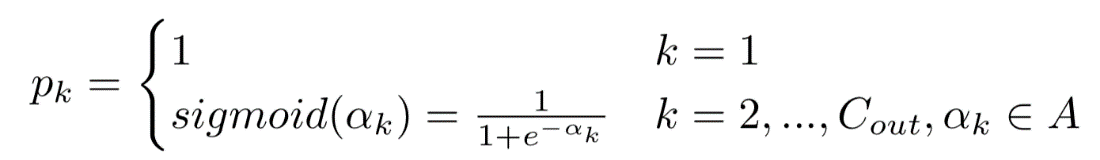（3）

其中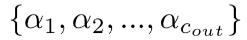是可學習的參數。在該方法中，每層至少保留了一個通道，因此p1 = 1。

步驟二、計算出每一個通道被保留的的邊緣概率p(wk)。

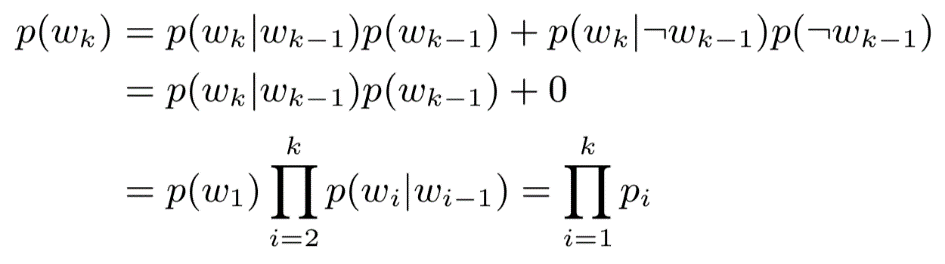（4）

由上述公式可以看出，邊際概率p(wk)可以被化簡為前k個轉移概率的乘積，并且隨著k的增大而減小。

步驟三、將每一個通道的邊緣概率與對應通道的輸出相乘，作為下一層的輸入。

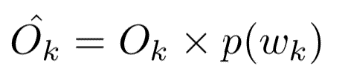（5）

若第k個通道的邊際概率趨于0，則表示該通道的輸出趨于0，從而可以被剪掉。通過這種建模方式，可以保證每一層中靠后的通道先會被剪枝。

(4) 訓練流程

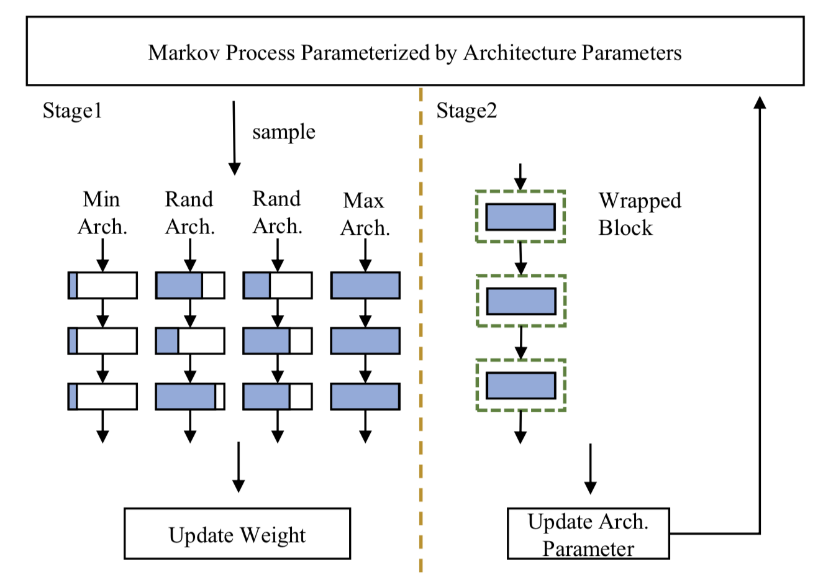
圖五 訓練流程示意圖

如圖五所示，DMCP的訓練可以分為兩個階段：訓練原模型和更新馬爾科夫模型。這兩個階段是交替進行來優化的。

階段一，訓練原模型。

在每一輪迭代過程中，利用馬爾科夫過程采樣兩個隨機結構，同時也采樣了最大與最小的結構來保證原模型的所有參數可以充分訓練。所有采樣的結構都與原模型共享訓練參數，因此所有子模型在任務數據集上的精度損失函數得到的梯度都會更新至原模型的參數上。

階段二，更新馬爾科夫模型

在訓練原模型后，通過前文中所描述的方法將馬爾科夫模型中的轉移概率和原模型結合，從而可以利用梯度下降的方式更新馬爾科夫模型的參數，其損失函數如下：

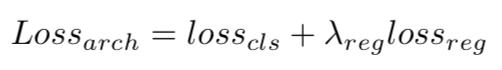（6）

其中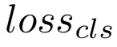為模型在任務數據集上的精度損失函數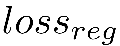，為計算量約束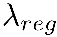，為超參數。這里我們使用了模型期望FLOPs來約束模型的計算量（實際應用中可以方便的換用latency等指標來約束模型的計算量），其損失函數如下:

（7）

上述等式中的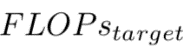為目標計算量，模型的計算量期望為每一層的計算量期望的總和。

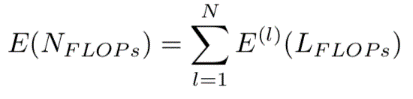（8）

實驗結果

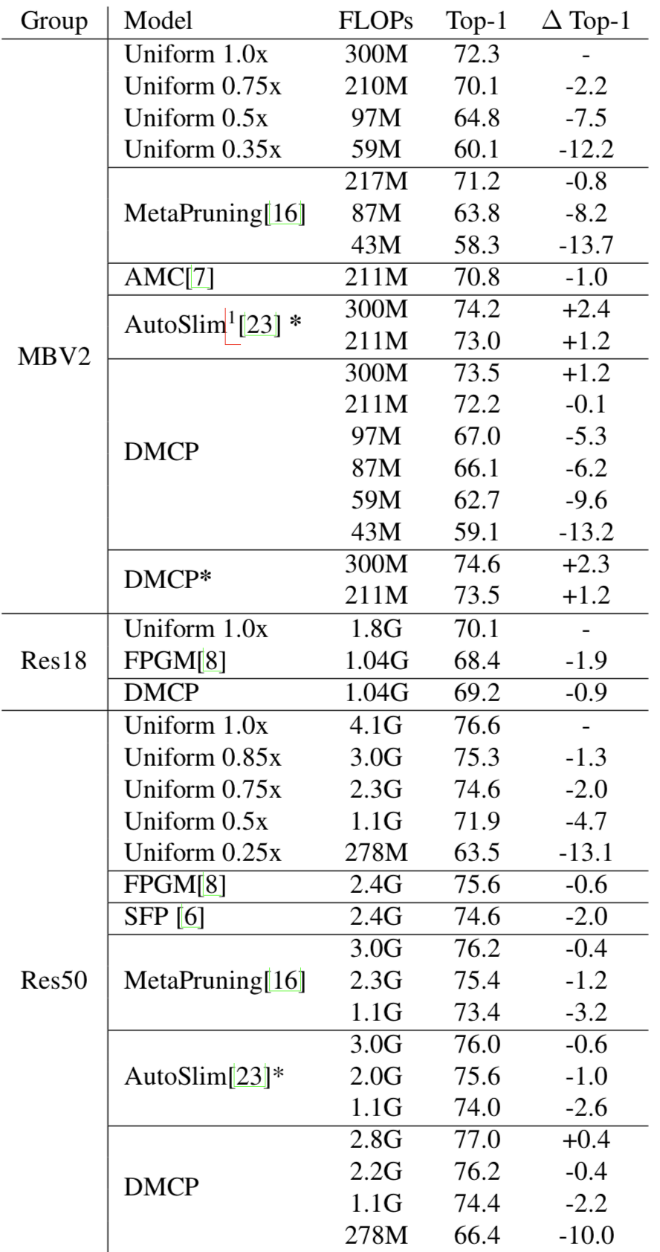
作者在ImageNet數據集上對比了其他最新模型剪枝方法，在各種計算量下，DMCP在MobileNet-v2和ResNet上均超過現有方法，如下表所示：

傳送門

DMCP代碼目前已經開源，歡迎各位同學使用和交流。

論文：DMCP: Differentiable Markov Channel Pruning for Neural Networks

論文作者：Shaopeng Guo, Yujie Wang, Quanquan Li, Junjie Yan

論文地址： https://arxiv.org/pdf/2005.03354.pdf

源碼地址：https:///github.com/zx55/dmcp

References

[1] Yann Le Cun, John S. Denker, and Sara A. Solla. Optimal brain damage. In Advances in Neural Information Processing Systems, pages 598–605. Morgan Kaufmann, 1990.

[2] Zhuang Liu, Mingjie Sun, Tinghui Zhou, Gao Huang, and Trevor Darrell. Rethinking the value of network pruning. arXiv preprint arXiv:1810.05270, 2018.

[3] Yihui He, Ji Lin, Zhijian Liu, Hanrui Wang, Li-Jia Li, and Song Han. Amc: Automl for model compression and ac- celeration on mobile devices. In Proceedings of the European Conference on Computer Vision (ECCV), pages 784– 800, 2018.

[4] Hanxiao Liu, Karen Simonyan, and Yiming Yang. Darts: Differentiable architecture search. arXiv preprint arXiv:1806.09055, 2018.

[5] echun Liu, Haoyuan Mu, Xiangyu Zhang, Zichao Guo, Xin Yang, Tim Kwang-Ting Cheng, and Jian Sun. Metapruning: Meta learning for automatic neural network channel pruning. arXiv preprint arXiv:1903.10258, 2019