ICLR 2021 | 點云網絡也能量化了？北航、商湯、UCSD 提出首個點云二值網絡 BiPointNet

近年來，神經網絡量化被視為一種有效的模型壓縮和加速手段，受到深度學習研究人員的廣泛關注。近日，機器學習頂會 ICLR 2021 接收論文結果已經正式公布，至少有 12 項工作展示了神經網絡量化方向的相關進展。本文將介紹首個應用二值量化的方法設計的高效點云深度學習模型 BiPointNet，這項研究工作由北京航空航天大學劉祥龍教授團隊、商湯新加坡研究團隊和加州大學圣迭戈分校共同完成。

隨著點云應用的不斷演進，用于點云的深度學習模型需要被部署在各類離線邊緣場景，如自動駕駛設備和手持移動設備等，這給模型的推理、存儲、傳輸等環節帶來了巨大挑戰。如何讓點云模型在邊緣設備上“又輕又快”，是工業界和學術界共同關注的重要問題。

我們的文章旨在解決邊緣設備上運行點云應用時的資源限制問題，并提出了第一個點云深度學習二值化模型 BiPointNet。BiPointNet 的準確率表現幾乎可以媲美全精度網絡，并在邊緣設備上帶來了14.7 倍的超高加速比和 18.9 倍的存儲節省，從模型量化的視角打開了點云模型硬件部署優化的新思路。

Part 1 背景及概述

隨著深度神經網絡模型能夠直接處理原始點云數據，點云學習已經取得了很大的進展。在實際應用場景下，這類網絡非常需要實時交互和快速響應，例如自動駕駛和增強現實等。但是，它們的部署環境通常是一些資源受限的邊緣設備。盡管研究者們已經提出了諸如 Grid-GCN，RandLA-Net 和 PointVoxel 之類的新穎的算法來加速點云網絡的處理，但是它們還是依賴于昂貴的浮點運算。模型二值化方法受益于輕量的二值化參數和高效的按位操作，已成為最有前景的模型壓縮加速方法之一，但是由于 2D 圖像和 3D 點云之間的根本性差異，現有的二值化方法無法被直接遷移到 3D 點云網絡中。

在本文中，我們提出了 BiPointNet，將全精度的點云網絡轉換成高效且準確的二值化模型 (整體框架圖見圖 1)。我們研究了二值化特征的信息熵和點云聚合函數的表現之間的關系：為了解決聚合后的二值化特征存在同質化的問題，提出了熵最大化聚合函數 (Entropy-Maximizing Aggregation，EMA)；提出了逐層尺度恢復 (Layer-wise Scale Recovery，LSR) 以有效地恢復輸出的尺度，并使得尺度敏感的結構可以正常運作。

圖 1: BiPointNet 的整體框架圖

Part 2 方法

點云非結構化（unstructured）的特征導致多層感知機是網絡中最常見的結構，而二值化模型包含的是二值化的多層感知機，能夠對輕量級的二值化權重和激活執行高效的位運算操作 (XNOR 和 Bitcount) ：

其中，和代表二值化激活與權重，表示基于位運算的向量內積。

2.2 熵最大化聚合函數

我們的研究表明，由于嚴重的同質化現象，聚合函數是二值化的一個性能瓶頸。

理想情況下，二值化張量 B 應該盡可能多地保留原始張量 Y 所包含的信息。而當最大池化層的輸入呈隨機分布時，二值化輸出的信息熵隨著聚合元素數量n趨近于無窮大而趨向于0。由于點的數量通常較大 (如ModelNet40 的分類任務的n為 1024 )，這導致不論輸入池化層的特征如何，其輸出特征總是高度相似的，如圖 2 所示。2D 視覺中聚合函數通常用較小的核(ResNet 和 VGG-Net 中使用  的池化核)，問題并不嚴重。因此，我們需要一類能夠使 B 的信息熵最大化的聚合函數，以避免聚合引起的特征同質化問題。

圖 2: 聚合引起的特征同質化問題

其中  表示聚合函數 (例如最大池化和平均池化)，  表示變換單元，可以有多種形式，我們發現最簡單的常數偏移已經十分有效。這個偏移將輸入進行移位運算以最大化二值化特征 B 的信息熵。BiPointNet 中的變換單元  可以被定義為 。當   表示最大池化時，目標函數的解與無關，從而規避了在點云應用中聚合元素數量 n 過大造成的特征同質化問題。

2.3 One-Scale-Fits-All: 逐層尺度恢復

在本節，我們闡述并解決了二值化會導致特征尺度失真的問題。

我們發現，當信息熵取到最大值時，輸出特征的尺度與特征通道數直接相關，因此造成尺度的不合理放大，即尺度失真。尺度失真使得一些為 3D 深度學習設計的對尺度較為敏感的結構失效（見圖 3），還導致前向傳播時的激活和后向傳播時的梯度趨于飽和。

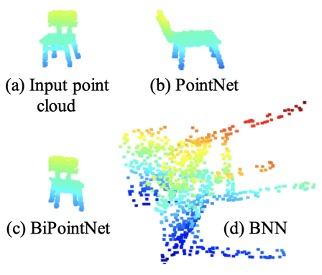
圖 3: 尺度失真

為了恢復輸出的尺度和調整能力，我們提出在 BiPointNet 的二值線性層中應用 LSR。我們設計了一個可學習的逐層尺度恢復因子 ，并通過二值線性層和全精度的輸出之間的標準差來初始化:

其中，表示標準差。而且在訓練過程中是可學習的。具有 LSR 的二值線性層的計算步驟如下:

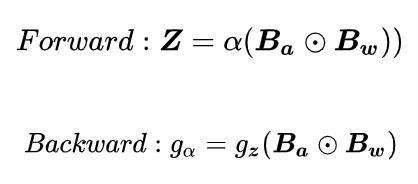
其中，和分別表示 a 和 z 的梯度。通過在 BiPointNet 中應用 LSR，我們緩解了由于二值化導致輸出尺度失真的問題。

Part 3 實驗

我們的實驗表明了 BiPointNet 在點云學習上的強大性能，部分設置下甚至媲美全精度模型。

表 1 中結果表明，同時使用EMA和LSR可以顯著縮小二值化模型和全精度模型之間的性能差距；在表 2 中，我們展示了 BiPointNet 優于其他二值化方法；表 3 展示了在幾種主流的點云深度學習模型中取得的提升。

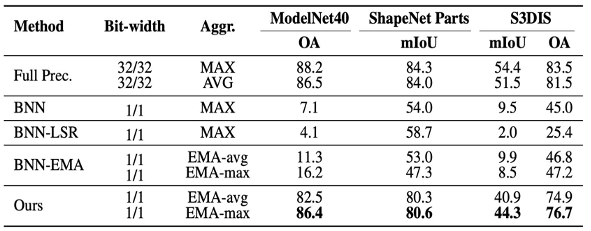
表 1: BiPointNet 在 ModelNet40 (分類)、

ShapeNet Parts (零件分割)、S3DIS (語義分割) 上的消融實驗

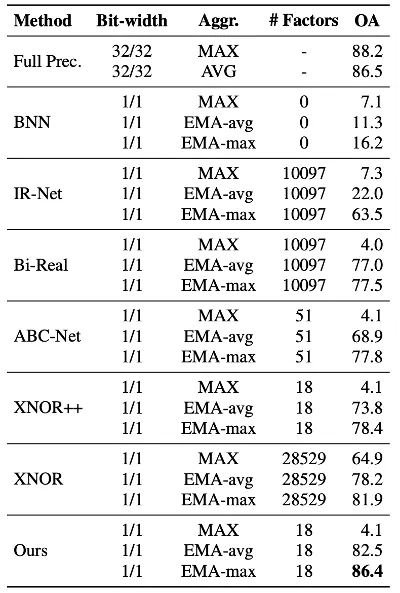
表 2: 基于 PointNet 的二值化方法對比

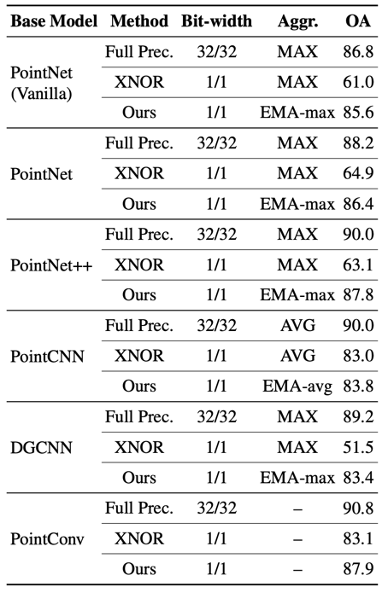
表 3: 在主流骨干網絡上應用我們的方法

為了驗證 BiPointNet 在真實世界的邊緣設備上的高效性，我們還將其部署在ARM CPU Cortex-A72 和Cortex-A53 的樹莓派上。盡管PointNet 已經是現有模型中公認的快速、輕量模型，BiPointNet依然帶來了14.7倍的推理加速和18.9倍的存儲節省。

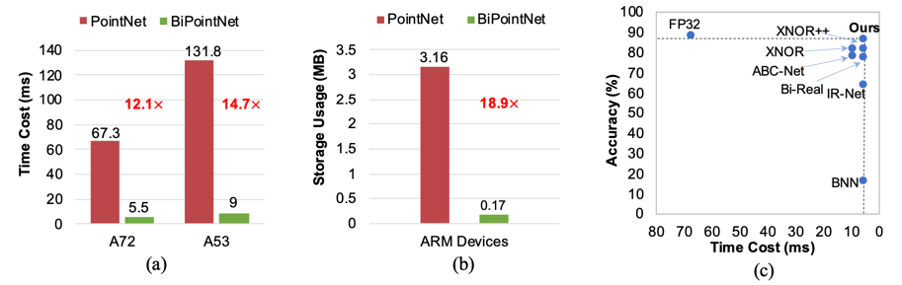
圖 5: (a) 耗時對比；(b) 存儲使用對比；(c) 不同二值化方案速度和準確率的關系散點圖